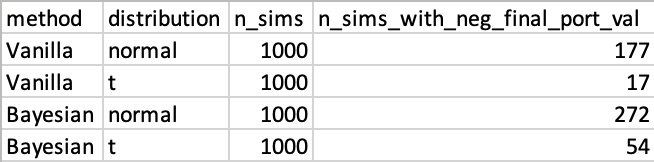Forecast Portfolio Growth with Markov Chain Monte Carlo Simulation
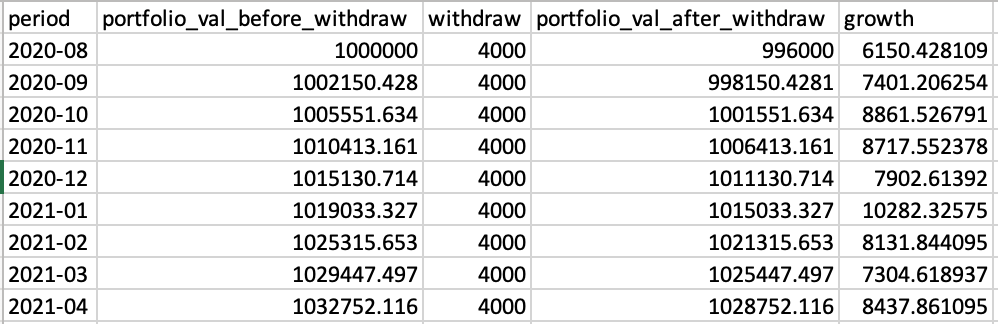
The client, a financial planning company, hired us to build a tool for projecting the spending down of a portfolio during post-divorce. For example, a 40 year old woman gets divorced and gets $1 million, which she invests in a portfolio of stocks and bonds. She needs a monthly living expense of $5000 for the first ten years, and $4000 for the rest of her life. She will get monthly child support of $600 for 10 years, and monthly alimony of $400 for 4 years. She will start receiving $1500 per month in Social Security in 27 years. How long will her portfolio last? How much income can she withdraw without spending the portfolio down at all?
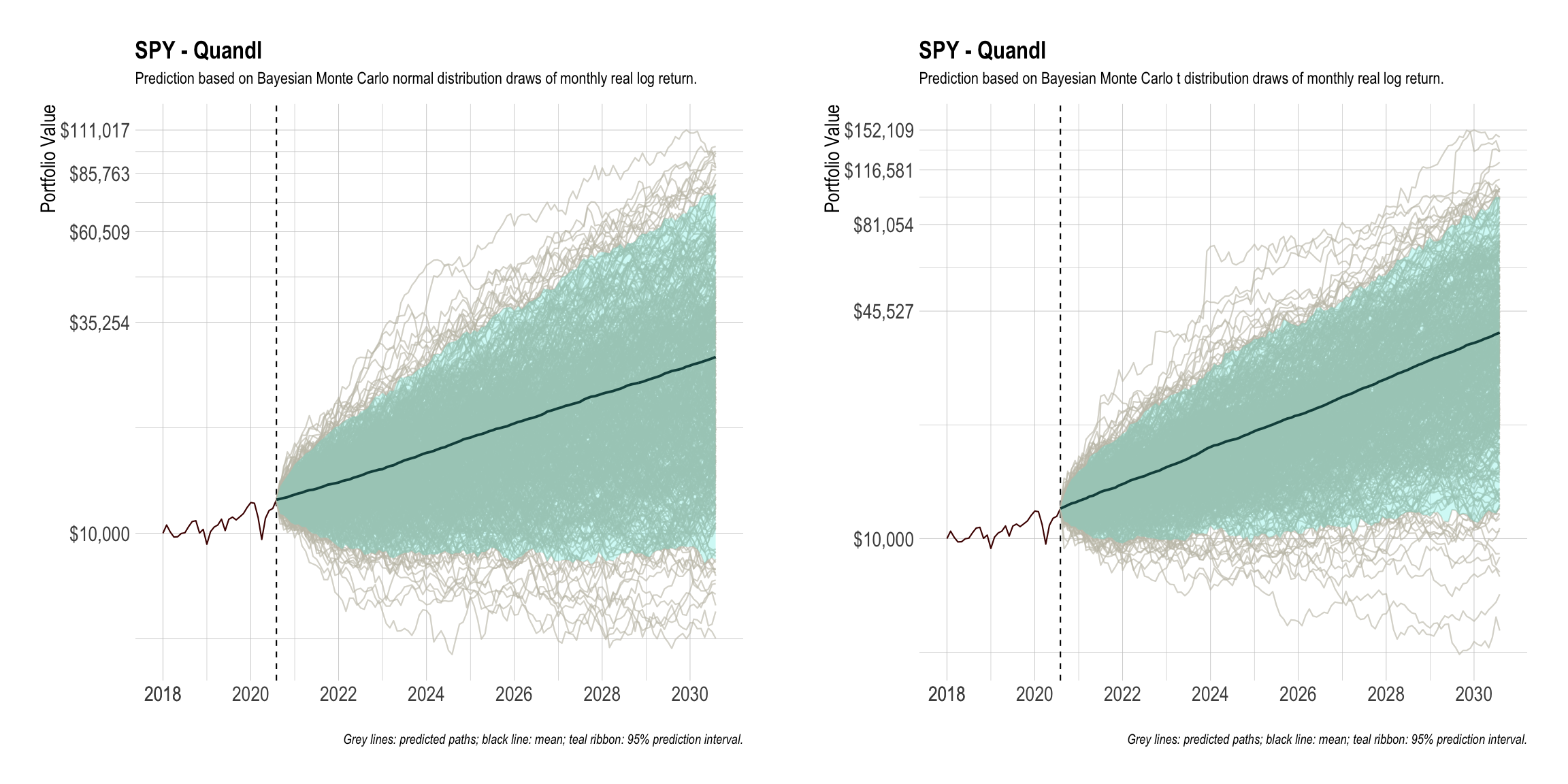
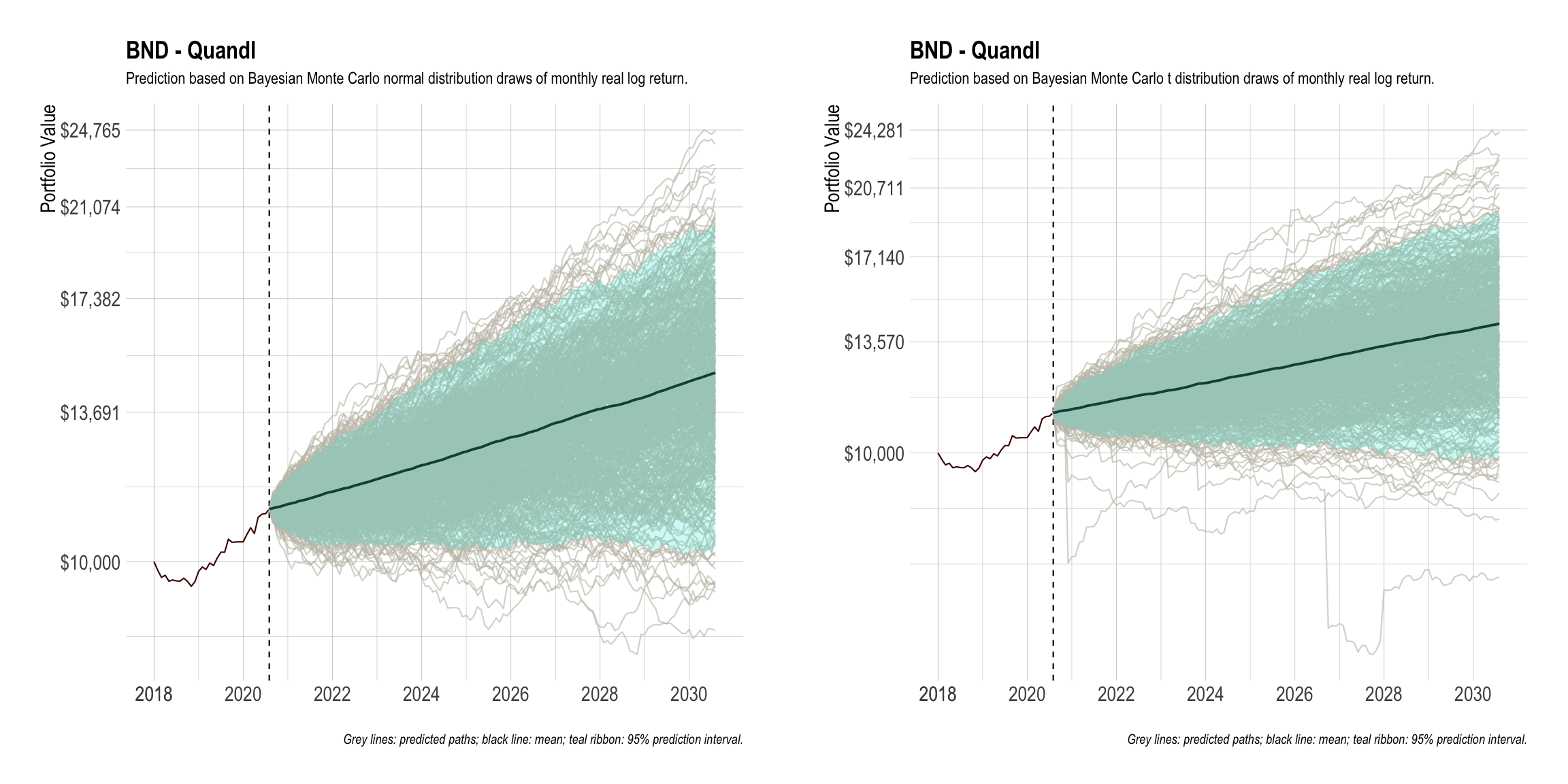
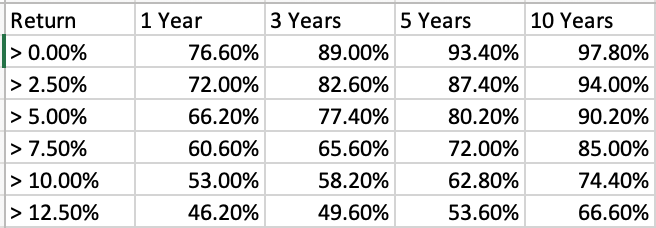
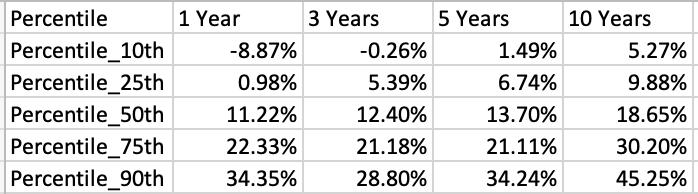
The key is to forecast the returns of the portfolio many years into the future. A naive approach is to use Monte Carlo simulation while assuming the annual returns are normally distributed. I programmed this approach along with a better alternative, namely, Markov Chain Monte Carlo (MCMC) simulation, in R and JAGS. In total, my tool has four methods for forecasting monthly returns:
- Naive Monte Carlo, assuming monthly returns follow a normal distribution.
- Naive Monte Carlo, assuming monthly returns follow a t distribution.
- MCMC, assuming monthly returns follow a normal distribution and a flat prior before the first month.
- MCMC, assuming monthly returns follow a t distribution and a flat prior before the first month (best).
My tool has the following features:
- Allow user to input initial portfolio value and specify when to retire.
- Allow user to set portfolio target allocations (e.g., 80/20 for S&P 500/Total Bond market).
- Automatically rebalance to target allocation every 12-month.
- Allow user to change allocation every 120 month (e.g., reduce stocks holdings by X% every 10 years).
- Allow user to manipulate time periods in which withdrawals are taken (e.g., withdraw $3000 per month for the first five years, and $2000 per month for the next ten years).
- Allow user to change the income at different periods in their lives (e.g., the more the income, the less they need to withdraw).
- Account for inflations.
The following screenshots show what the output look like: